Prakitsche Anwendung der Ableitung – Teil 1

Wenn man mit dem Thema "Bestimmung der Ableitung von Funktionen" anfängt, kommt immer die Frage vor "Aber wozu braucht man überhaupt die Ableitung?"

Es gibt viele Anwendungsprobleme für die Ableitung einer Funktion. In diesem Artikel habe ich typische Probleme/Fragestellungen ausgewählt. Der Artikel ist in vier Teile strukturiert, die jeweils eine kurze Erklärung mit Bespiel und Links zu weiteren Fragen + Lösungen enthalten.

Inhaltsübersicht

Teil 1: Steigung, Steigungswinkel, Tangente und Normale

Teil 2: Hoch-, Tief-, Wendepunkte und Wendetangenten einer Funktion

Teil 3: Schneidung bzw. Berührung zweier Funktionen

Teil 4: Extremwertprobleme

---

Teil 1: Steigung, Steigungswinkel, Tangente und Normale

A. Wiederholung der Begriffe

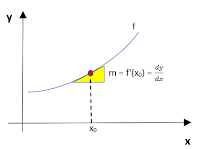
Steigung Die Steigung einer Funktion (auch Anstieg m genannt) ist ein Maß dafür, wie steil der Graph einer Funktion an einer gewissen x-Stelle ansteigt (m > 0) oder abfällt (m < 0). Der Spezialfall (m = 0) bedeutet, dass sich an dieser x-Stelle ein Extrempunkt (also ein Maximum oder ein Minimum) der Funktion befindet. Es kann dort aber auch ein Sattelpunkt vorliegen. Wir werden Extrempunkte in Teil 2 dieses Artikels untersuchen!

Steigungswinkel Der Steigungswinkel gibt an, in welchem Winkel eine Gerade zur x-Achse steht. Aus der Steigung m erhält man den Steigungswinkel α mit:  m = tan(α)    =>    α = tan-1(m)

Tangente und Normale Die Tangente ist eine Gerade, die den Graphen einer Funktion an einem Punkt P berührt. Dabei ist die Steigung der Tangente gleich die Steigung der Funktion an diesem Berührungspunkt. Die Normale ist die Senkrechte zur Tangente durch den Berührungspunkt P.

Wiederholung der Ableitungsregeln

Wenn Sie bei den Aufgaben die Ableitungsregeln nachschlagen möchten, können Sie diese im Artikel "Zusammenfassung und Beispiele zu den Differentiationsregeln (Ableitungsregel)" finden.

B. Beispiel

C. Weitere Aufgaben

Ich hoffe, Sie haben diesen Artikel hilfreich gefunden!

Für weitere Übungen können Sie mein Aufgabenpaket kostenlos herunterladen. Es enthält unterschiedliche Fragestellungen zum Thema "Steigung, Steigungswinkel, Tangente und Normale".

Außerdem können Sie alle Aufgabenpakete zum Thema Ableitung in unserem Store kostenlos herunterladen.

Verpassen Sie keine zukünftigen Beiträge, indem Sie uns folgen.

 

Ihre Fragen bzw. Kommentare sind immer willkommen!